En physique, on appelle « force » l’action d’un objet sur un autre.
Il n’existe pas de force toute seule. Elles vont toujours par deux. L’ensemble de ces deux forces s’appelle une interaction.
En physique, on appelle « force » l’action d’un objet sur un autre.
Il n’existe pas de force toute seule. Elles vont toujours par deux. L’ensemble de ces deux forces s’appelle une interaction.

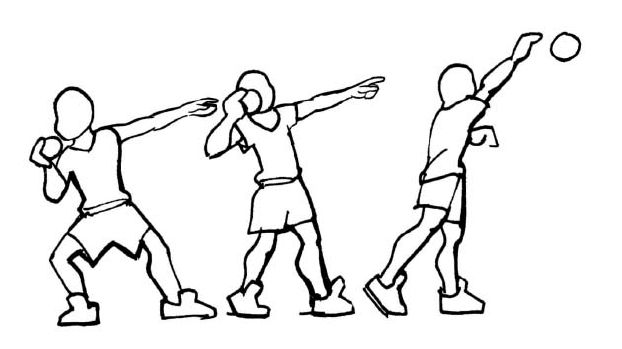
Exemple rameur. Nageur qui fait le crawl qui pousse l’eau vers l’arrière. Détente d’un basketeur
Qu’est ce qui agit sur quoi ? L’eau part en arrière, le bateau part en avant.
Lorsqu’un objet A agit sur un autre objet B, alors l’objet B agit sur l’objet A. C’est ce qu’on appelle une interaction (=actions entre eux)
assets/3eLoi_apesanteur.mp4 “3e loi dans l’ISS” V0VCVlRUDQoNCjAwOjAwOjA2LjUwMCAtLT4gMDA6MDA6MDguNjkwDQpPbiBwZXV0IHZvaXIgcXUnaWxzIGZsb3R0ZW50DQoNCjAwOjAwOjA4Ljc2MCAtLT4gMDA6MDA6MTEuOTcyDQpMYSBwb3Vzc8OpZSBxdSdpbHMgZXhlcmNlbnQgbGVzIMOpbG9pZ25lIGwndW4gZGUgbCdhdXRyZQ0KDQowMDowMDoxNC45MTIgLS0+IDAwOjAwOjE4LjAyMg0KQWxleGFuZGVyIHBvdXNzZSBQZWRybyA6IGFjdGlvbg0KDQowMDowMDoxOC4zNjggLS0+IDAwOjAwOjIxLjEyNA0KQ2VsYSBmYWl0IGJvdWdlciBQZWRybyA6IHLDqWFjdGlvbi4NCg0KMDA6MDA6MjEuNDk0IC0tPiAwMDowMDoyNS41MTQNCkVuIG3Dqm1lIHRlbXBzIFBlZHJvIHBvdXNzZSBBbGV4YW5kZXIgOiBhY3Rpb24uLi4NCg0KMDA6MDA6MjUuODg0IC0tPiAwMDowMDoyOS41NTgNCi4uLiBmYWlzYW50IGFsbGVyIFBlZHJvIGRhbnMgbGEgZGlyZWN0aW9uIG9wcG9zw6llIDogcsOpYWN0aW9uDQoNCjAwOjAwOjI5LjkyOCAtLT4gMDA6MDA6MzIuODQ4DQpJbHMgc2Ugc29udCDDqWxvaWduw6lzIGRlIGxhIG3Dqm1lIGRpc3RhbmNlIDoNCg0KMDA6MDA6MzIuOTcyIC0tPiAwMDowMDozNS42MjINCmwnYWN0aW9uIGVzdCDDqWdhbGUgw6AgbGEgcsOpYWN0aW9uLg==
Qu’est-ce qu’une force|C’est l’action d’un objet sur un autre.
Qu’est-ce qu’une interaction|Actions reciproques entre deux objets.
Lorsqu’un objet agit sur un autre, il effectue une action. Il existe deux types d’action :
Quels sont les deux types
d’actions|<ul><li>l'action de contact (quand les objets doivent se toucher)</li><li>l'action à distance (quand les objets <strong>ne doivent pas nécessairement se toucher</strong>).</li></ul>

15’
entraînement DIO
Comment sont les doubles flèches dans un
DIO ?|<ul><li>en trait plein pour les interactions de contact</li><li>en pointillés pour les interactions à distance.</li></ul>
DIO nous permet d’identifier les forces. Maintenant on veut représenter les forces appliquées à l’objet d’étude.
Montrer ressort à vide sur potence, puis avec une masse accrochée.
20’

Comment écrit-on symboliquement une force
exercée par un objet A sur un objet
B ?|<svg width="10ex" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="-.2 -.2 32.9 21.3"><defs><path id="d" d="M4.4-7v-.3s0-.2-.2-.2l-.1.1L.6 2.1v.2l.1.2c.2 0 .2 0 .3-.2l3.4-9.4Z"/><path id="c" d="M1.8-1.1c-.4.6-.8.8-1.2.8-.2 0-.3 0-.3.2l.2.1h1.8s.2 0 .2-.2l-.1-.1c-.3 0-.5-.1-.5-.4L2-1l.8-1.3h2.5l.1 1.7c0 .3-.5.3-.7.3-.1 0-.2 0-.2.2l.1.1H7s.2 0 .2-.2L7-.3c-.7 0-.7 0-.7-.4l-.6-6.2c0-.2 0-.2-.2-.2l-.2.1-3.5 6ZM3-2.6 5-6l.3 3.3H3Z"/><path id="e" d="M1.6-.8c-.1.4-.1.5-1 .5 0 0-.2 0-.2.2l.3.1h3.5C5.8 0 7-1.2 7-2.2c0-.7-.6-1.2-1.6-1.4 1-.1 2.1-.9 2.1-1.8 0-.8-.6-1.4-1.8-1.4H2.3c-.2 0-.3 0-.3.2l.3.1h.4c.2 0 .3 0 .3.2v.2L1.5-.8ZM3-3.6l.6-2.5c.1-.4.1-.4.6-.4h1.2c1 0 1.1.6 1.1 1a2 2 0 0 1-2 1.9H3ZM2.7-.3h-.3l-.1-.1v-.2L3-3.4h2c.9 0 1 .7 1 1.1 0 1-.8 2-2 2H2.7Z"/><path id="b" d="M4.3-4.7h1.3c1.1 0 1.2.3 1.2.7a3.1 3.1 0 0 1-.1.8l.1.2C7-3 7-3 7-3.3l.8-3.3-.1-.2-.2.3C7.2-5.4 6.9-5 5.7-5H4.4l.9-3.7c.1-.5.2-.6.7-.6h2c1.8 0 2 .6 2 1.6v1.1c.2 0 .2 0 .3-.3l.3-2.5v-.2c0-.2-.1-.2-.4-.2H3.4c-.3 0-.4 0-.4.3l.3.1c1 0 1 .1 1 .3l-.1.3-2 7.7c0 .5-.1.7-1.1.7-.3 0-.4 0-.4.2s0 .2.2.2h3.7s.2 0 .2-.3l-.4-.1c-1 0-1.1-.1-1.1-.3V-1l1-3.7Z"/><path id="a" d="M7.7-8.6c-.2.2-.7.7-.7.9l.2.3c.2 0 .2-.1.3-.3l1-.9c.2 0 .3 0 .3-.2s0-.2-.2-.3c-.4-.3-.5-.7-.5-.8 0-.2 0-.3-.3-.3 0 0-.3 0-.3.2s.1.5.4.9H3.1c-.3 0-.5 0-.5.3 0 .2.3.2.5.2h4.6Z"/></defs><g transform="matrix(1.13 0 0 1.13 -64 -61)"><use x="58.5" y="64" xlink:href="#a"/><use x="56.4" y="67.7" xlink:href="#b"/><use x="65.5" y="70.2" xlink:href="#c"/><use x="73" y="70.2" xlink:href="#d"/><use x="78" y="70.2" xlink:href="#e"/></g></svg>
Comment représente-t-on une force sur un schéma ?|avec un segment fléché
Quelles sont les 4 caractéristiques d’une
force ?|<ul><li>point d'application</li><li>direction</li><li>valeur</li><li>sens</li></ul>
Où doit on placer le point d’application d’une
force
?|<ul><li>au point de contact pour une interaction de contact</li><li>au centre de l'objet pour une interaction à distance.</li></ul>
Faire le DIO puis représenter les forces qui s’appliquent aux objets suivants :




3 p212
Une force se mesure avec un dynamomètre. Elle s’exprime en newton (N).
Avec quel appareil mesure-t-on une force ?|un dynamomètre
Quelle est l’unité (et le symbole) de la force ?|le newton (N)
deux dynamomètres étalonnés par groupe un morceau de ficelle

8 (sauf 2.a), 10, 11 p213
Une force peut modifier un mouvement (sa vitesse ou sa direction) ou déformer un objet.
Si les forces qui s’exercent sur un objet se compensent, l’objet est soit immobile, soit en mouvement rectiligne uniforme.

Que peut-on dire du mouvement de ces objets ? Sachant qu’initialement :
Expliquer ce qu’est une équivalence avec :
Exemple : un palet de Hockey sur une patinoire :
14 p214
assets/newtons-first-lawmp4.mp4
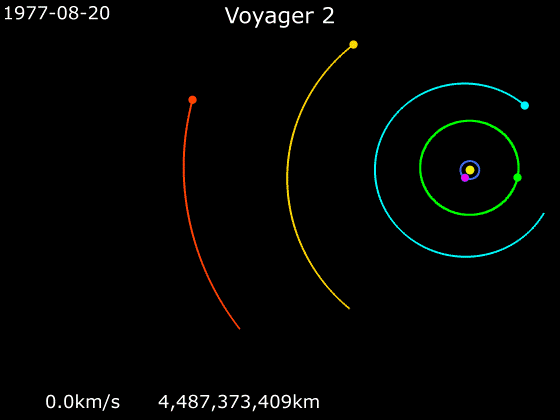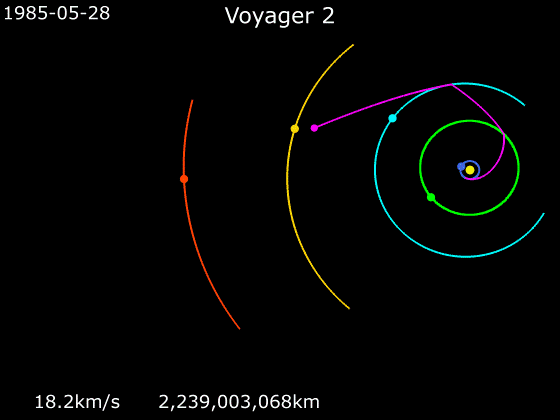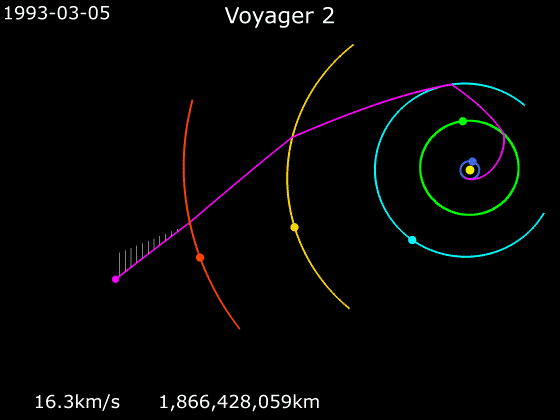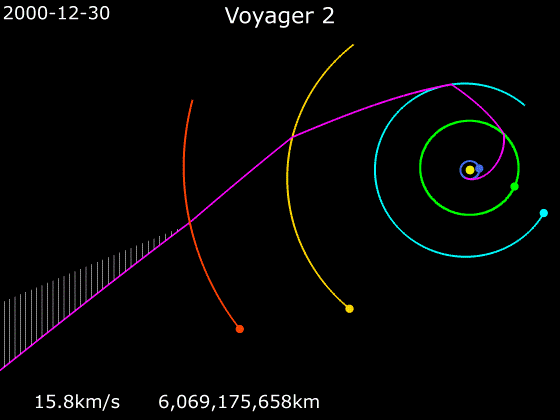
Les forces se compensent : le palet a un mouvement rectiligne uniforme.


Que peut-on dire du mouvement d’un objet qui ne
subit aucune
force ?|l'objet est immobile <strong> ou</strong> en mouvement rectiligne uniforme
Que peut-on dire des forces qui s’exercent sur un objet en mouvement rectiligne uniforme, ou immobile ?|Les forces se compensent, ou bien elles sont nulles.
15 p214, 18 p215